algorithms / Permutations playground

>>> Read full article

Get the example project here

If you’d like to try it out on your device:

Download and install Permutations-Playground.apk

In my Internet travels, I came across a coding question that looks something like this:

Find the number of permutations of string A in string B

• String A (search term): bcba
• String B (search data): babcabbacaabcbabcacbb

The idea is that the characters in the search term are compared in every permutation to the characters in the search data to identify how many instances can be found.

Although it seems kind of simple, the brute force approach of looping through every permutation of the search term for every permutation of each frame of data in the search data ends up being O(n!) factorial complexity which is pretty much useless for anything.

I can’t recall the exact place where I originally found this question - it might have come from Career Cup or something.

Anyway, it looked like an interesting problem to try and solve - in particular to try out different approaches to see which Java data structures work OK and which ones seemd to be able to do the calculations the fastest.

algorithms / Dijkstra's Algorithm - Part 2

>>> Read full article

Get the example project here

If you’d like to try it out on your device:

Download and install Treasure-Crab.apk

This post continues on from my Dijkstra’s Algorithm - Part 1 post. In this part we will put together a basic Android app to visualize the pathfinding. Let’s call the app Treasure Crab. The goals for the app are to:

• Display a graph along with an agent who needs to travel the shortest distance to reach the goal. The agent for this demo will be a crab and the goal will be a treasure chest.
• Allow the user to choose from some preset graphs.
• Create an render loop to show the agent moving to the goal in real time.
• Implement the ability to interact with the graph using touch to move the nodes around.
• Implement the ability to serialize and deserialize the graph so it can remember how we left it.

algorithms / Dijkstra's Algorithm - Part 1

>>> Read full article

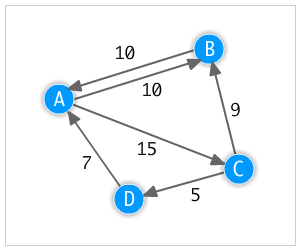
Get the example project here

So there’s probably a bunch of ways to do path finding but I wanted to try out Dijkstra’s algorithm using a basic graph structure.

In this post I’ll show examples of:

• Creating a simple directed, weighted graph.
• Writing an implementation of Dijkstra’s algorithm to run against the graph to find the shortest paths between nodes.

I’ll walk through some basic building blocks for making a graph in general as well.