So there’s probably a bunch of ways to do path finding but I wanted to try out Dijkstra’s algorithm using a basic graph structure.
In this post I’ll show examples of:
I’ll walk through some basic building blocks for making a graph in general as well.
We will need a few data models in order to construct the graph system. In particular:
For this post, we will be creating a weighted, directed graph, which means each edge will have a weight value, representing the cost (in this example the distance) of traversing between two nodes.
Because this will be a directed graph, an edge from a first node to a second node will not necessarily mean that there is a connection from the second node back to the first node.
A node will have a collection of edges which represent which neighbouring nodes can be reached.
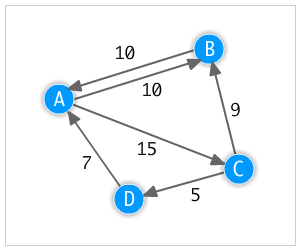
The picture at the top of this blog post is of a super basic directed, weighted graph, like what we are going to create:
Node class
public class Node {
// Unique identifier for this node.
private String mKey;
// Collection of all connections to other nodes.
private Map<Node, Edge> mEdges;
// The total distance from this node to an 'origin'
// node, used for path finding.
private double mPathFindingDistanceFromOrigin;
// A reference to a 'parent' node used for path finding.
private Node mPathFindingParentNode;
// Whether this node is considered to be 'complete' in
// respect to path finding.
private boolean mIsPathFindingComplete;
public Node(@NonNull String key) {
mKey = key;
mEdges = new HashMap<>();
}
/**
* Adding an edge will connect this node with the target
* node and record the weight of that edge.
*
* @param target node to connect to.
* @param weight between this node and the target node.
*/
public void addEdge(@NonNull Node target, double weight) {
if(mEdges.containsKey(target)) {
return;
}
mEdges.put(target, new Edge(target, weight));
}
@NonNull
public String getKey() {
return mKey;
}
@NonNull
public Map<Node, Edge> getEdges() {
return mEdges;
}
/**
* Resetting the node is used for path finding to clear
* any previously calculated path finding data and get
* ready for a new path finding calculation.
*/
public void resetPathFindingData() {
mPathFindingDistanceFromOrigin = Double.POSITIVE_INFINITY;
mPathFindingParentNode = null;
mIsPathFindingComplete = false;
}
public double getPathFindingDistanceFromOrigin() {
return mPathFindingDistanceFromOrigin;
}
@Nullable
public Node getPathFindingParentNode() {
return mPathFindingParentNode;
}
/**
* Updating a node is used for path finding, where the parent node and
* distance from origin will be determined during the algorithm and
* quite possibly be updated multiple times as the shortest paths are
* discovered.
*
* @param parentNode to reference for back tracking to an origin node.
* @param distanceFromOrigin the total distance from the origin to this node.
*/
public void updatePathFindingData(@Nullable Node parentNode, double distanceFromOrigin) {
mPathFindingParentNode = parentNode;
mPathFindingDistanceFromOrigin = distanceFromOrigin;
}
/**
* Is this node considered 'complete' for path finding.
*
* @return true if the node is 'complete'.
*/
public boolean isPathFindingComplete() {
return mIsPathFindingComplete;
}
/**
* Mark this node as 'complete' for path finding.
*/
public void setPathFindingComplete() {
mIsPathFindingComplete = true;
}
}
Edge class
public class Edge {
private Node mTarget;
private double mWeight;
public Edge(@NonNull Node target, double weight) {
mTarget = target;
mWeight = weight;
}
public double getWeight() {
return mWeight;
}
@NonNull
public Node getTarget() {
return mTarget;
}
}
Graph class
public class Graph {
private Map<String, Node> mNodes = new HashMap<>();
/**
* In this example we will just create a new node
* if we ask for one that doesn't exist.
*
* @param key to find.
*
* @return the node with the given key or a new one.
*/
@NonNull
public Node getNode(@NonNull String key) {
Node result = mNodes.get(key);
if(result == null) {
addNode(key);
return mNodes.get(key);
}
return result;
}
/**
* Add a new node with the given unique node key into
* the graph. Passing a node key that already exists
* will replace it.
*
* @param key of the node to add.
*/
public void addNode(@NonNull String key) {
mNodes.put(key, new Node(key));
}
/**
* Connecting nodes will create a new edge between the origin node
* and the target node, and assign the edge with the given weight.
*
* @param originKey to connect from.
* @param targetKey to connect to.
* @param weight of the edge between the two nodes.
*/
public void connectNodes(@NonNull String originKey, @NonNull String targetKey, double weight) {
Node origin = mNodes.get(originKey);
Node target = mNodes.get(targetKey);
if(origin == null || target == null) {
return;
}
origin.addEdge(target, weight);
}
/**
* Before running a path finding algorithm over the nodes
* in the graph, this method should be called to reset all
* the nodes back into their default state for path finding.
*/
public void resetPathFindingData() {
for(Node node : mNodes.values()) {
node.resetPathFindingData();
}
}
}
Populating the graph
Now that we have the basic building blocks for our graph system, we can populate the graph with nodes and edges. The following code will populate a new instance of our graph class so it matches the diagram shown earlier.
Notice that we first put all the nodes into the graph, then one by one connect them to all the other nodes that they can reach along with the weight representing the cost of each connected edge.
Graph graph = new Graph();
// Populate all the nodes for the graph.
graph.addNode("A");
graph.addNode("B");
graph.addNode("C");
graph.addNode("D");
// Connect each node to it's neighbours.
graph.connectNodes("A", "B", 10.0);
graph.connectNodes("A", "C", 15.0);
graph.connectNodes("B", "A", 10.0);
graph.connectNodes("C", "B", 9.0);
graph.connectNodes("C", "D", 5.0);
graph.connectNodes("D", "A", 7.0);
The algorithm
Cool! We have a graph - but it is pretty useless at the moment. The next thing we will do is to write an implementation of Dikjstra’s algorithm such that we can pick a starting origin node and find the shortest path to any other node in the graph.
I’m not going to explain how the algorithm works here, there are a number of articles on the net for it, but it is worth watching this YouTube clip that I found quite good in explaining the theory.
The basic pseudo is that:
INPUT: ORIGIN NODE, TARGET NODE
OUTPUT: PATH STRUCTURE CONTAINING THE STEPS TO TRAVEL FROM ORIGIN TO TARGET
Create a new *set* to track the *visited nodes*.
Create a new *priority queue* that will be the source for the remaining nodes to evaluate.
Add the *origin* node to the *visited nodes* and the *priority queue*.
While there are nodes still in the *priority queue*
Get the next node as *current node* from the *priority queue* and mark it as *complete*
OPTIONAL:
If *current node* is the *target node* Then
Break from the While loop because we've just found the shortest path to the *target* node.
End if
For each *edge target node* in the *current node*
If the *edge target node* is already marked as *complete* Then
Skip the *edge target node*
Else
Calculate the distance from the *origin* to the *edge target node*
If the *visited nodes* already contains the *edge target node* Then
if the calculated distance is smaller than the distance stored
in the *edge target node* then update the *edge target node* with
the new calculated distance and set its parent to *current node*.
Else
Add the *edge target node* to the *visited nodes* with the calculated
distance and set its parent to *current node*
End if
Add the *edge target node* to the *priority queue*
End if
End for
End while
If the *target node* we want to reach is not in the *visited nodes* Then
No path can be found from the *origin node* to the *target node*
Else
Create a *path* structure to hold the final path
Add the *target node* to the *path*
While the *target node* has a *parent*
Add the *parent node* to the *path*
Assign the *target node* to its *parent node*
End while
The *path* will now hold a stack of nodes that represents
how to travel from the *origin node* to the *target node*,
in order and by the shortest distance.
End if
Below is an example of the algorithm - although it seems a bit wordy and dense, it isn’t too difficult to follow:
public class DijkstrasAlgorithm {
/**
* Attempt to calculate the shortest path between the
* given origin node and target node.
*
* It is assumed that all nodes in the underlying graph
* are in a 'path finding reset' state before running this algorithm.
*
* @param origin to start from.
* @param target to attempt to find the shortest path to.
*
* @return a path structure representing the shortest path, or
* null if no path to the target could be found.
*/
@Nullable
public Path findPath(@NonNull Node origin, @NonNull Node target) {
// The visited nodes track each node that has been visited, and will also
// contain the distances and parent node information.
Set<Node> visitedNodes = new HashSet<>();
// The priority queue is very important because it allows us to add nodes into
// it which will automatically be placed in order based on their distance from
// the origin. Because of this, we can always guarantee that the first item in
// the queue is the one with the minimum distance.
PriorityQueue<Node> remainingNodes = new PriorityQueue<>(10, new Comparator<Node>() {
@Override
public int compare(Node a, Node b) {
if(a.getPathFindingDistanceFromOrigin() > b.getPathFindingDistanceFromOrigin()) {
return 1;
}
if(a.getPathFindingDistanceFromOrigin() < b.getPathFindingDistanceFromOrigin()) {
return -1;
}
return 0;
}
});
origin.updatePathFindingData(null, 0.0); // Configure the origin node.
visitedNodes.add(origin); // Put the origin node into the visited nodes.
remainingNodes.offer(origin); // Put the origin node into the queue.
// Dequeue nodes as long as there are nodes left.
while (!remainingNodes.isEmpty()) {
// Grab the next node from the queue, which should be the
// next minimum distance node from the origin.
Node currentNode = remainingNodes.poll();
// Since it is the first item in the priority queue, it
// should be the next minimum distance node, mark it as
// completed.
currentNode.setPathFindingComplete();
// Short circuit! If we just discovered the target
// node in a completed state, then there is no
// reason to keep finding paths to the rest of the
// nodes - we are done! If you want to calculate *all*
// the shortest paths from the origin to *every* other
// reachable node, you wouldn't short circuit here.
if(currentNode == target) {
break;
}
// Loop through all the edges from the current node,
// which represent its neighbours.
for(Edge edge : currentNode.getEdges().values()) {
// Find out what the target node for this edge is
Node edgeTarget = edge.getTarget();
// If we've already 'completed' the edge target, skip it ...
if(edgeTarget.isPathFindingComplete()) {
continue;
}
// Calculate how far it is from the origin to the edge target,
// which will be the current node's distance plus the weight
// of the edge we are looking at inside this loop.
double distanceToEdgeTarget = currentNode.getPathFindingDistanceFromOrigin() + edge.getWeight();
// If the edge target has already been visited...
if(visitedNodes.contains(edgeTarget)) {
// and our current calculated distance is smaller than the distance
// already stored in the edge target ...
if(distanceToEdgeTarget < edgeTarget.getPathFindingDistanceFromOrigin()) {
// then adopt the calculated distance and the current node as its parent node ...
edgeTarget.updatePathFindingData(currentNode, distanceToEdgeTarget);
// and update the set of visited nodes.
visitedNodes.remove(edgeTarget);
visitedNodes.add(edgeTarget);
}
} else {
// Otherwise, this edge target has never been visited before, so
// simply adopt the calculated distance and current node as its parent ...
edgeTarget.updatePathFindingData(currentNode, distanceToEdgeTarget);
// and add it to the set of visited nodes.
visitedNodes.add(edgeTarget);
}
// Add the edge target to the priority queue, which will take into
// account its distance from the origin when deciding where to
// place it in the queue. The result will be that if this particular
// edge target had the smallest distance, it will be in the first
// position in the queue.
remainingNodes.add(edgeTarget);
}
}
// At this stage, we will have our visited nodes data full with
// the shortest paths between the origin node and all other nodes,
// so find the target node in the visited nodes and walk backwards
// through its parent nodes to build the actual path that the caller
// was looking for.
Node stepNode = target;
// If the target node is not in the visited nodes collection, then it
// must have never been visited (was unreachable from the origin).
if(!visitedNodes.contains(stepNode)) {
return null;
}
// Otherwise create a new path to generate an ordered step
// by step path from the origin to the target.
Path path = new Path();
// Add the target node initially.
path.addStep(stepNode.getKey());
// Capture what the total distance was to the target.
path.setTotalDistance(stepNode.getPathFindingDistanceFromOrigin());
// Iterate backward through each parent node, adding it to
// the path until we hit the origin.
while(stepNode != null && stepNode.getPathFindingParentNode() != null) {
path.addStep(stepNode.getPathFindingParentNode().getKey());
stepNode = stepNode.getPathFindingParentNode();
}
// This will contain the stack of steps to follow to travel
// from the origin node to the target node in the minimum
// distance found in the graph.
return path;
}
/**
* Representation of the path found as a
* result of running the algorithm, with a
* stack of node keys used to store a path.
*/
public static class Path {
private final Stack<String> mPathKeys;
private double mTotalDistance;
public Path() {
mPathKeys = new Stack<>();
}
/**
* Add a 'step' with a node key.
*
* @param nodeKey of the next step in the path
* from the origin to the target.
*/
public void addStep(@NonNull String nodeKey) {
mPathKeys.add(nodeKey);
}
/**
* Capture the total distance found from the origin
* to the target.
*
* @param totalDistance from the origin to the target.
*/
public void setTotalDistance(double totalDistance) {
mTotalDistance = totalDistance;
}
/**
* Retrieve the completed path from the origin
* to the target, which can be followed to
* travel the shortest path.
*
* @return the path of node keys that can be used
* to travel the shortest distance from the origin
* to the target.
*/
@NonNull
public Stack<String> getPath() {
return mPathKeys;
}
/**
* The shortest distance found from the origin
* to the target.
*
* @return distance from the origin to the target.
*/
public double getTotalDistance() {
return mTotalDistance;
}
}
}
How to use it
To use our new algorithm we basically just make sure that all the nodes in our graph are in a reset state, then create an instance of Dijkstra’s algorithm and call its find path method.
For example, to find the path between the origin node B and the target node D:
// ... create and populate a graph instance.
graph.resetNodes();
// Choose our *origin* and *target* nodes
Node originNode = graph.getNode("B");
Node targetNode = graph.getNode("D");
// Create the algorithm and run its find path method with the given origin and target.
DijkstrasAlgorithm.Path path = new DijkstrasAlgorithm().findPath(originNode, targetNode);
// If the path result was null, then no path could be found.
if(path == null) {
printLine("No path could be found...");
} else {
Stack<String> steps = path.getPath();
StringBuilder sb = new StringBuilder("Path: ");
while (!steps.isEmpty()) {
sb.append(" > ");
sb.append(steps.pop());
}
printLine(sb.toString());
printLine("Total distance: " + path.getTotalDistance());
}
The output for this example would be:
Path: > B > A > C > D
Total distance: 30.0
In Dijkstra’s Algorithm - Part 2 we’ll make something slightly more interesting with the algorithm!