If you’d like to try it out on your device:
Download and install Permutations-Playground.apk
In my Internet travels, I came across a coding question that looks something like this:
Find the number of permutations of string A in string B
The idea is that the characters in the search term are compared in every permutation to the characters in the search data to identify how many instances can be found.
Although it seems kind of simple, the brute force approach of looping through every permutation of the search term for every permutation of each frame of data in the search data ends up being O(n!) factorial complexity which is pretty much useless for anything.
I can’t recall the exact place where I originally found this question - it might have come from Career Cup or something.
Anyway, it looked like an interesting problem to try and solve - in particular to try out different approaches to see which Java data structures work OK and which ones seemd to be able to do the calculations the fastest.
I enjoyed doing this because it let me play with some structures that I don’t normally get to use, including Tries which I think are pretty cool.
My plan of attack was:
After spending some time on it, I came up with four different approaches:
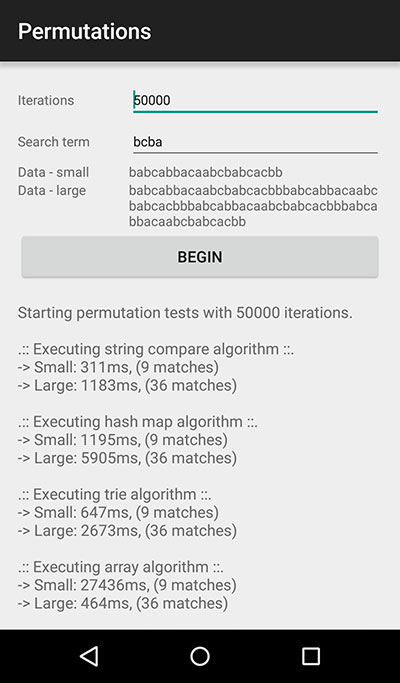
Before diving into the detail, here is a benchmark of running the four different approaches. Each algorithm was executed with the main processing loop running 50,000 times on a Nexus 5.
Each algorithm was permitted to do some configuration setup before running the loop.
Running benchmarks like this is a bit academic, but at least they provide a contrast across approaches within the same control environment in a given scenario:
| Algorithm | Time - small | Time - large |
|---|---|---|
| Array with sorted comparison | 470ms | 1200ms |
| Character hash map with visit tracking | 1200ms | 5700ms |
| Trie with sorted input | 600ms | 2600ms |
| Custom array hash table | 140ms | 500ms |
The algorithms use a few helper classes to know how to return the result of running and store data during operation. Here are the classes that you will see used in the algorithm code:
CharacterNode.java
public class CharacterNode {
/**
* The instance count refers to
* how many times this particular
* character node is permitted to
* be queried before being considered
* an invalid choice.
*/
public int instanceCount;
/**
* A tracking variable used to know
* how many times something has
* 'visited' the node - used for
* finding unique matches to characters,
* and should be reset to 0 before each
* evaluation cycle.
*/
public int visitedCount;
}
PermutationMatch.java
public class PermutationMatch {
private int mStartIndex;
private int mEndIndex;
public PermutationMatch(int startIndex, int endIndex) {
mStartIndex = startIndex;
mEndIndex = endIndex;
}
public int getStartIndex() {
return mStartIndex;
}
public int getEndIndex() {
return mEndIndex;
}
}
AlgorithmResult.java
public class AlgorithmResult {
private long mTotalTimeTaken;
private int[][] mMatches;
private int mCursor;
/**
* Given a number of maximum matches possible
* by the algorithm, construct a result matches
* array with a fixed size.
*
* @param maximumMatches to create the fixed size
* matches array with.
*/
public AlgorithmResult(int maximumMatches) {
mMatches = new int[maximumMatches][2];
}
/**
* Move the cursor back to the start.
*/
public void reset() {
mCursor = 0;
}
/**
* A permutation result can be identified by storing
* the start and end array indices into its source
* data collection.
*
* @param start index of this permutation.
* @param end index of this permutation.
*/
public void addResult(int start, int end) {
mMatches[mCursor][0] = start;
mMatches[mCursor][1] = end;
// Advance the internal cursor
mCursor++;
}
/**
* Walk the matches array up to the position
* of the internal cursor and return the result.
*
* @return list of permutation match objects.
*/
public List<PermutationMatch> getResults() {
List<PermutationMatch> result = new ArrayList<>();
for(int i = 0; i < mCursor; i++) {
result.add(new PermutationMatch(mMatches[i][0], mMatches[i][1]));
}
return result;
}
public long getTotalTimeTaken() {
return mTotalTimeTaken;
}
public void setTotalTimeTaken(long totalTimeTaken) {
mTotalTimeTaken = totalTimeTaken;
}
}
In this algorithm, the search term is initially sorted, then a frame is moved across the search data, each time sorting the characters in the frame and doing an Arrays.equals against the sorted search term.
The main cost of this algorithm was needing to do an array copy and a sort on every iteration in order to be able to compare the search term to the frame each time.
ArrayWithSortingAlgorithm.java
public final class ArrayWithSortingAlgorithm {
public static AlgorithmResult execute(int iterations, @NonNull String searchTerm, @NonNull String searchData) {
long startTime = System.currentTimeMillis();
AlgorithmResult result = new AlgorithmResult(searchData.length());
// We need to create a sorted version of the search term
// because an easy way to see if a string is a permutation
// of another string is to sort them both then see if they
// match, which is what this algorithm will do.
char[] sortedSearchTerm = searchTerm.toCharArray();
int searchTermLength = sortedSearchTerm.length;
Arrays.sort(sortedSearchTerm);
// Convert our search data string into a character array
// to make it easier to loop over.
char[] searchDataCharacters = searchData.toCharArray();
int searchDataLength = searchDataCharacters.length;
// We will use a data 'frame' to hold the characters to
// examine as we step through the data.
char[] frame = new char[searchTermLength];
// Execute the algorithm as many times as we were asked to.
for(int iteration = 0; iteration < iterations; iteration++) {
result.reset();
// Step through each frame of data in the search data
for (int i = 0; i < searchDataLength - searchTermLength + 1; i++) {
System.arraycopy(searchDataCharacters, i, frame, 0, searchTermLength);
Arrays.sort(frame);
// If string inside our sorted frame matches our search term
// then this range of the data is a permutation of the search term.
if (Arrays.equals(sortedSearchTerm, frame)) {
result.addResult(i, i + searchTermLength);
}
}
}
result.setTotalTimeTaken(System.currentTimeMillis() - startTime);
return result;
}
}
In this algorithm, the characters in the search term are initially stored in a lookup table (hash map), along with how many instances of each character there are. Then a frame is moved through the search data and the characters in the frame are validated against the lookup table.
If a character is found in the character hash map, it is then also checked against how many times the particular character has been visited in the iteration.
If the character has already been visited more than the instance count for that character, it fails validation and marks the frame as ineligible to be a permutation.
The main cost of this algorithm was needing to reset all the visited states on each iteration, due to the need to iterate over a map. Using a LinkedHashMap did help a small amount vs a regular HashMap but it was still slow.
CharacterHashMapAlgorithm.java
public final class CharacterHashMapAlgorithm {
public static AlgorithmResult execute(int iterations, @NonNull String searchTerm, @NonNull String searchData) {
long startTime = System.currentTimeMillis();
AlgorithmResult result = new AlgorithmResult(searchData.length());
char[] searchDataCharacters = searchData.toCharArray();
// Create a new lookup table in the form of a linked hash map.
// I used the linked hash map here because it is faster when
// iterating through its elements than a regular hash map.
Map<Character, CharacterNode> lookupTable = new LinkedHashMap<>();
// Inflate the lookup table with the characters
// in the search term.
for(char c : searchTerm.toCharArray()) {
CharacterNode node = lookupTable.get(c);
// If the character node isn't already in the
// lookup table, then create and add it.
if(node == null) {
node = new CharacterNode();
lookupTable.put(c, node);
}
// By maintaining an 'instance count' we
// will be able to know when there are
// duplicate characters in the search term,
// and therefore also know how many times
// something can 'visit' the character when
// evaluating the algorithm before being
// considered a failed match.
node.instanceCount++;
}
int searchTermLength = searchTerm.length();
int range = searchDataCharacters.length - searchTermLength + 1;
for(int iteration = 0; iteration < iterations; iteration++) {
result.reset();
// Iterate through the input data up to the point
// where the 'frame' of data would go out of scope.
for (int i = 0; i < range; i++) {
boolean found = true;
// We need to reset the 'visited' counter for
// each character node before evaluating.
for(Map.Entry<Character, CharacterNode> entry : lookupTable.entrySet()) {
entry.getValue().visitedCount = 0;
}
// Step through each of the characters within a
// 'frame' of data within the input data
for(int j = i; j < i + searchTermLength; j++) {
// See if we have a match in the lookup table
CharacterNode node = lookupTable.get(searchDataCharacters[j]);
// If there was no match, or we've already visited
// this character node more times than permitted
// by the instance count, then this is a failed match.
if(node == null || node.visitedCount >= node.instanceCount) {
found = false;
break;
}
// Increment this character node's 'visited' counter. A node is
// only permitted to be visited up to its 'instance count'
// before rejecting validation against it.
node.visitedCount++;
}
// If we reached this point, then we successfully found
// a permutation match!
if(found) {
result.addResult(i, i + searchTermLength);
}
}
}
result.setTotalTimeTaken(System.currentTimeMillis() - startTime);
return result;
}
}
In the trie algorithm, the characters in the search term are initially sorted and used to construct a trie. Then a frame is moved through the search data, and each frame of data is first sorted, then validated against the trie to identify if there is a match.
Although the actual request to validate a character array within a trie is considerered to be O(k) where k is the length of the string to search for, unfortunately this algorithm still required each frame to be copied and sorted before querying the trie.
A trie is fantastic when used for multiple search terms or when decoupled from this kind of scenario, but not so hot in this particular scenario - but not really the fault of the trie itself.
The code for this one is a little bit long because it also contains the definition of the trie structure.
TrieAlgorithm.java
public final class TrieAlgorithm {
public static AlgorithmResult execute(int iterations, @NonNull String searchTerm, @NonNull String searchData) {
long startTime = System.currentTimeMillis();
AlgorithmResult result = new AlgorithmResult(searchData.length());
// Prepare the search term by turning it into a character
// array and sorting it.
char[] searchTermCharacters = searchTerm.toCharArray();
int searchTermLength = searchTermCharacters.length;
Arrays.sort(searchTermCharacters);
// Create a new trie to store our dictionary which in
// this scenario is just a single word.
Trie trie = new Trie();
trie.addWord(searchTermCharacters);
// Prepare the search data and tracking fields.
char[] searchDataCharacters = searchData.toCharArray();
int range = searchDataCharacters.length - searchTermLength + 1;
char[] frame = new char[searchTermLength];
for(int iteration = 0; iteration < iterations; iteration++) {
result.reset();
for (int i = 0; i < range; i++) {
// Populate our 'frame' of data for this evaluation.
System.arraycopy(searchDataCharacters, i, frame, 0, searchTermLength);
// Sort the 'frame' so it will match if it is a permutation.
Arrays.sort(frame);
// Ask the trie to find the sorted word in our data 'frame'. Because
// it is sorted then the trie should be able to step from character
// to character in order to determine if there is a permutation match.
if (trie.findWord(frame)) {
result.addResult(i, i + searchTermLength);
}
}
}
result.setTotalTimeTaken(System.currentTimeMillis() - startTime);
return result;
}
/**
* Basic trie used to store our search term. Normally
* a trie would be used to store dictionaries of many
* words because they provide an O(1) lookup time for
* any given word, however this example we will only
* have 1 word in it.
*/
private static class Trie {
private TrieNode mRoot;
public Trie() {
mRoot = new TrieNode();
}
public boolean findWord(@NonNull char[] data) {
TrieNode node = mRoot;
// Starting from the root node of the trie,
// walk through the hash map of each child
// that contains the next character in the
// sequence. If we attempt to move to a
// character that isn't in the current
// node's children, then the word doesn't
// exist in the trie.
for (char c : data) {
node = node.getChildren().get(c);
if(node == null) {
return false;
}
}
// If we successfully travel to the final
// character in the data, we need to know
// if the node we landed on is considered
// to be an 'end node' - meaning it was
// the terminating character for a word
// that was inflated into the trie when
// it was initially constructed.
return node.isEndNode();
}
public void addWord(@NonNull char[] word) {
TrieNode node = mRoot;
// Add each character to the child hash
// maps of each node as needed. A character
// will only be added if it is found to be
// non existent in a leaf node, thereby
// forming the trie data structure.
for(char c : word) {
if(node.getChildren().containsKey(c)) {
node = node.getChildren().get(c);
} else {
node = node.addCharacter(c);
}
}
// The final character in an inserted word
// is marked as the 'end' so it can be
// identified as the terminal character in
// trie word lookups.
node.setIsEndNode(true);
}
public static class TrieNode {
private Map<Character, TrieNode> mChildren = new HashMap<>();
private boolean mIsEndNode;
@NonNull
public Map<Character, TrieNode> getChildren() {
return mChildren;
}
public TrieNode addCharacter(@NonNull Character character) {
TrieNode node = new TrieNode();
mChildren.put(character, node);
return node;
}
public void setIsEndNode(boolean isEndNode) {
mIsEndNode = isEndNode;
}
public boolean isEndNode() {
return mIsEndNode;
}
}
}
}
This was the most complex of the algorithms to write, but the speed benefits are obvious.
The characters in the search term are converted to their integer representations and a lookup table is generated based on the resulting integer positions, with a maximum length of the highest integer value identified in the search term.
The trick to this is that any given character can be turned into its integer representation by subtracting ‘0’ from it:
char c = 'a';
int v = c - '0'; // v == 49
Then a frame is moved through the search data, and each character in the frame has its integer representation calculated which is then used to perform a look up in the lookup table.
This algorithm allowed me to completely avoid copying arrays and sorting anything. The only minor trade off was that the lookup table was sparse, meaning that it contained many empty data slots between the integer representations of the characters from the search term.
Overall it was pretty cool to get this running fairly quickly and shows that a bit of extra effort can pay off.
ArrayNoSortingAlgorithm.java
public final class ArrayNoSortingAlgorithm {
private ArrayNoSortingAlgorithm() { }
public static AlgorithmResult execute(int iterations, @NonNull String searchTerm, @NonNull String searchData) {
long startTime = System.currentTimeMillis();
AlgorithmResult result = new AlgorithmResult(searchData.length());
int searchTermLength = searchTerm.length();
// Cache the integer representation of each
// character in the search term so we can use
// them as indices into the larger array of
// 'character nodes'.
int[] searchTermValues = new int[searchTermLength];
int maxSearchTermValue = 0;
for(int i = 0; i < searchTermLength; i++) {
searchTermValues[i] = searchTerm.charAt(i) - '0';
// If the integer value of the character is
// the highest we've encountered yet, remember
// it so after we can create a 'sparse' array of
// the discovered max length.
if(searchTermValues[i] > maxSearchTermValue) {
maxSearchTermValue = searchTermValues[i];
}
}
// Create a 'sparse' array holding the search term
// 'character nodes' at the indices of their values.
CharacterNode[] lookupTable = new CharacterNode[maxSearchTermValue + 1];
// Loop through each of the search term values (which are
// the integer values of the original characters).
for (int searchTermValue : searchTermValues) {
// Get the character node at the value index
CharacterNode node = lookupTable[searchTermValue];
// If it is null, then we've never created one yet
// so make a new one and put it into the array slot
if (node == null) {
node = new CharacterNode();
lookupTable[searchTermValue] = node;
}
// A new node will have an instance count of 1,
// however if the same character value node is
// updated, it will have its instance count
// incremented. The instance count is critical
// to the algorithm because it will determine
// how many times the same character can be
// considered a 'match' when processing an
// input frame of data compared to the search
// term. Because the search term might have
// duplicate characters in it, having an
// instance count allows us to know exactly
// *how many* of each character it has.
node.instanceCount++;
}
char[] searchDataCharacters = searchData.toCharArray();
int range = searchDataCharacters.length - searchTermLength + 1;
for(int iteration = 0; iteration < iterations; iteration++) {
result.reset();
// Loop through the input data up to a point where the
// 'frame' of data would go out of scope.
for (int i = 0; i < range; i++) {
boolean found = true;
// Reset the visitCount node counters first by iterating through
// the integer values of the search term and using the values
// as a position index into the larger lookup table.
for(int j = 0; j < searchTermLength; j++) {
lookupTable[searchTermValues[j]].visitedCount = 0;
}
// Loop again to determine if the current 'frame' of data is in
// the data set, based on the lookup table position index which
// is derived by calculating the integer value of the character
// being evaluated in the search data.
for(int k = i; k < i + searchTermLength; k++) {
int characterIndex = searchDataCharacters[k] - '0';
// It is possible (and likely probable) that a
// character is encountered in the search data
// that has an integer value outside the
// lookup table's length. The reason is that the
// lookup table will only be as long as the highest
// search term integer value.
//
// If this happens then obviously the character doesn't
// match any of our search term characters, otherwise
// the lookup table would range up to the value.
if(characterIndex >= lookupTable.length) {
found = false;
break;
}
// If we reach this point, get the node from the lookup table
// at the index position matching the search data character
// integer value.
CharacterNode node = lookupTable[characterIndex];
// If there is no such node for the given character integer value
// or the node that is there has already been visited the maximum
// number of times, then this 'frame' of data is not a match.
if(node == null || node.visitedCount >= node.instanceCount) {
found = false;
break;
}
// Increment the 'visit' counter for this particular node
// so it can be evaluated again against its 'instance count'.
node.visitedCount++;
}
// If we reach this point, then the currently evaluated
// character does in fact exist uniquely in the search term!
if(found) {
result.addResult(i, i + searchTermLength);
}
}
}
result.setTotalTimeTaken(System.currentTimeMillis() - startTime);
return result;
}
}
During the process of writing up the algorithms, I tried to also include a cache based on a hash set to identify when a frame of characters was being evaluated that had already been identified as a permutation.
The idea was that each iteration, the frame was converted to a string, allowing a cache lookup. The problem became apparent though that converting a character array to a string on every iteration cost more than the benefit of the cache itself.
I took the cache back out - perhaps on larger data sets it might have started to show its value but crazily all it did was slow things down!
Also, I had to employ a kind of cursor approach to adding matching permutations to the result (see the AlgorithmResult class). Initially I had a regular List<> field that I added permutations to as I discovered them, however I found it taking a large performance hit to construct the new objects and ultimately resize the backing ArrayList as the data was cleared and expanded.
Instead, I kept an array of arrays, with the key array having a fixed size equal to the length of the search data string. By doing this, I was able to add permutation results in O(1) time every time, with zero new allocations. A cursor field managed the position in the array so every call to addResult would place the permutation data at the current cursor position and then increment the cursor position.
I got the idea from Android cursors which kind of work a little bit like that.
I actually enjoyed this exercise and learned some things about the performance characteristics of a few commonly used Java data structures.
END